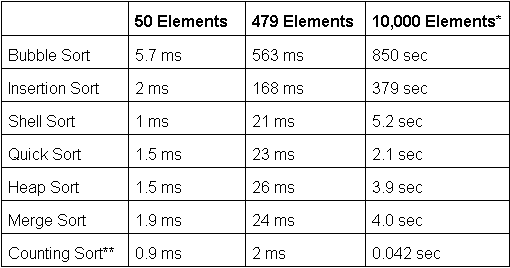
There are a number of sort algorithms available that can be adapted for use in Cicode. This article explains how several of them work, including their pros, cons, and sample code. Also considered is how to sort more elements than Cicode arrays can handle, sorting a table by more than one column, and sorting international characters. All of the referenced code is contained in the attached sort.ci file.

1. Bubble Sort

BubbleSort() is an exchanging sort. It constantly compares each element with the one below it and exchanges them if necessary. This causes the lowest strings (alphabetically) to ‘bubble’ to the top. Although easy to understand, it is extremely inefficient unless the list is already sorted, and it should not normally be used.

2. Insertion Sort

InsertionSort() compares the first two elements in the list and swaps them if necessary (so they are alphabetical). Then it compares the 3rd element with each one above it and swaps it if necessary so all 3 elements are alphabetical. Next, it compares the 4th element with each one above it, and so on, until the end of the list is reached.

This algorithm is fast for small lists and lists that are already mostly sorted. It is often used to finish off the sorting when using complex sort algorithms that break the list into multiple small lists. Unfortunately, the sort time quadruples each time the list size doubles.

3. Shell Sort

ShellSort() compares two values, and swaps them if one value is smaller than the other. It starts the comparisons at a calculated distance (‘gap’) from the top of the array, instead of just comparing consecutive elements. Calculating the optimal gap size speeds up the sort considerably. One calculation method is shown in the attached sample function.

Shell Sort uses the insertion method, but it moves elements more efficiently than Insertion Sort and is generally much faster (especially for large lists). ShellSortEx() has been modified to support 10,000 or more strings using multiple arrays, which makes it slower, however.
           
4. Quick Sort

QuickSort() picks an element in the array as a pivot point, or partition. It swaps the other elements until all the elements before the partition are lower alphabetically, and all the elements after the partition are higher alphabetically. Now there are effectively two lists, but neither is alphabetical yet. The function then calls itself recursively to repeat the process on each of the new, smaller, lists. This repeats until there is only one element in each list. At this point the entire array is alphabetical.

This is normally one of the fastest sorting methods, but in some cases (such as a list that is mostly alphabetical or has many duplicates), it can be as slow as Insertion Sort. This can be improved by using different methods to choose the pivot point and by using Insertion Sort when the partition contains 9 or fewer items. An alternate version of Quick Sort is attached which doesn’t use recursion. Although it requires an extra integer array, it eliminates the Cicode stack overflows caused by the recursive version of Quick Sort.
           
5. Heap Sort

With HeapSort() the array elements are organized into a heap, then it is sorted. In a heap each element has a parent element above it and 0, 1, or 2 child elements under it. The root element is the highest alphabetically and each child element is less than or equal to it’s parent. If any child is greater than it’s parent, they’re swapped. Once the heap is complete, the root (first) element gets swapped with the last element and dropped from the heap. Then the process repeats with alphabetical elements building up from the end of the array to the beginning.

Heap Sort is nearly as fast as Quick Sort, and it doesn’t require recursion. Another benefit is that it doesn’t suffer from the slow worst-case that Quick Sort has. Because of it’s complexity however, it may not outperform Quick sort or even Shell Sort unless the list is very large (approximately 5,000+ items).
           
6. Merge Sort

Merge Sort starts by comparing pairs of strings and swapping them if they’re out of order. Then it merges each list of two items into a list of 4 items, and so on until they have all been merged into one list.

A sample Merge Sort function is shown below. To avoid Cicode stack overflows it uses the bottom-up variation which doesn’t require recursion. However, it does require an extra string array large enough to temporarily hold the items being sorted.
           
7. Counting Sort

Counting sort puts numbers (not strings) in order by finding their correct position based on a count of the occurrences of each number. First, the minimum and maximum value are found in the input array. An intermediate array is used to record the number of occurrences of each input value. This is converted into the element number where the occurrences of each value should begin in the output array. Then, the input values are copied to the correct locations in the output array.

This can be by far the fastest of the above sorting methods because it does not compare values. However it can only be used in specific situations. It only works with integer values, not strings. Its speed depends on the number of values to sort, and the range of those values. Since integer arrays can have 15,359 elements, it can sort that many elements, and the difference between the lowest and highest value must be less than 15,359.

The attached example uses a different array for the output values. It could be modified to write them back to the input array, but performance would suffer somewhat. If the minimum and maximum values of the data are known they can be passed to the function to save time. Otherwise, they are calculated. If the range is too great, error 259 (Array Overrun) is returned.

Using the Sample Cicode Functions

To use the attached sample functions, follow these steps:
1. Call EnterCriticalSection("SortAlgorithm"). This is necessary so the global array is not used by 2 threads at once (see Q3402).
2. Fill the global array with up to 479 strings (the maximum number of elements allowed in Citect string arrays—see Q1128).
3. Call the sort function. Pass the first and last element numbers that were filled with data so it is not necessary to clear out other data left in the array by a previous sort.
4. Read all the strings back out of the array.
5. Call LeaveCriticalSection("SortAlgorithm") so other threads are allowed to use it.
           
Sort Stability

The Insertion, Bubble, and Merge sort algorithms are ‘stable’, in that they will maintain the original order for strings that are equal. Shell, Heap, Quick, and Counting sort are not stable. This does not matter for sorting a single array, but it does if there are two arrays to keep in sync. For example, there may be a list of alarm tags in one array and a list of alarm priorities in another array. One of the stable sort algorithms could be modified to sort one array but keep the other one in sync with it. The user would sort one list (keeping the other in sync), then sort the other list (keeping the first one in sync). The alarms will now be sorted primarily by priority, but all alarms with the same priority will be sorted by name also.

MergeSort2() shows how the Merge Sort algorithm can be modified to use two arrays. When calling it, specify whether it should sort by array 1 or 2.

Indexed Sorting

Instead of re-ordering the strings in the original array, the sort algorithm can create an index array and sort that. This leaves the original array untouched and is faster than making a copy of the entire array and sorting the copy. The ShellSortIdx() function uses the Shell sort algorithm to do index sorts. The index array is a list of integers, with each index element containing the element number of the corresponding item in the string array. For example, to read the first string using the index, use the command: sFirstItem = gsSortArray[gnIndex[0]]

Sort Algorithm Performance

Each method was compared on a Compaq EVO P4 2GHz PC with CitectSCADA 6.10 SP A and Windows XP. Random, 8-character strings were generated and sorted by each method. The sorting time was averaged over multiple sorts with different strings each time.


           
* The functions (except Counting Sort) were modified to use multiple arrays for the 10,000 item tests. See the attached ShellSortEx() function and supporting functions SortItemGet() and SortItemSet() to read and write items.
** Counting Sort was tested with random integer values where the minimum value was 0 and the maximum value was 500.
           
The performance of each function can change depending on (1) whether the list is actually random or has already been partially sorted, (2) how many duplicate items exist, (3) the data type being sorted, (4) if an external string compare function is used, (5) if a second array must be kept in sync, (6) if multiple arrays are needed to contain the list. It would be good to test with real data from the target system to find the best-performing algorithm.

The SleepMS() function could be added to the main loops in the sort functions to prevent them from using all available CPU time.
           
Data Types

The sample functions (excluding Counting Sort) all sort string arrays. However, they can be modified to sort numbers by changing the STRING variable declarations to REAL or INT. Counting Sort is inefficient for strings unless they only need to be sorted by the first character or two.
           
International Characters

The above sort functions use the Cicode ">" and "<" (greater than and less than) operators to compare strings. This is a quick and easy method and is case-insensitive, but it is only useful for non-accented English characters. For other characters, it simply compares their position in the ANSI character table. So, if the list contained the words "aberrant", "Ânonner", "ânonner", "éclaircir", "Éclaircir", and "Yammer", they are sorted as:
           
1. Aberrant
2. Yammer
3. Ânonner
4. Éclaircir
5. ânonner
6. éclaircir
           
Fortunately, Windows knows how to correctly compare international strings. It even takes into consideration differences in locale. For example, in traditional Spanish "ch" is between "c" and "d", but in Czech it comes after "h". To take advantage of this knowledge, use the Windows CompareString API function instead of the ">" operator. See the Microsoft Platform SDK documentation for CompareString to learn about its operation and options.

ShellSortI() uses CompareString via a wrapper function called StrCompare. StrCompare could be used similarly to make any of the other algorithms internationally aware. Because of the overhead of making DLL calls, however, performance will be lower. This version of Shell Sort took 4.9 ms to sort 50 strings and 92ms to sort 479 random strings.
           
An alternate version of StrCompare() is included that will work in older versions of Citect. The code is commented out so it will not be used by default. It is more complicated as it has to use the old DllCall() function. Because the list of parameters must be combined into one string, it has to make 2 DLL calls to sort strings over 118 characters, which makes it slower.

Array Size

String arrays can contain up to 479 strings (see Q1128). To store and sort more items in one list, the list needs to be broken up into multiple arrays. Intermediate Cicode functions are needed to read/write the values by determining which array/element each item number belongs to (e.g. Item 480 is array 2, element 0). The attached file contains SortItemGet() and SortItemSet() functions set up to handle 10,058 items in 21 arrays. ShellSortEx() has been modified to use these functions, although any of the sort functions could be modified to do so.

It is possible to store an unlimited number of strings in one list using Quexxx functions, however it is much slower. See Q4569 for an example.

References

"A Better Shell Sort: Part I" by Romke Soldaat
http://msdn.microsoft.com/library/default.asp?url=/library/en-us/dnoffpro01/html/ABetterShellSortPartI.asp
           
Visual Basic 6 from the Ground Up by Gary Cornell. Published by Osborne/McGraw-Hill.
           
Wikipedia article “Sorting Algorithm”
http://en.wikipedia.org/wiki/Sorting_algorithm