|
Statistic/Symbol |
Description |
Formula |
|
|
The sigma value estimated from the data. Also called Short Term Sigma. |
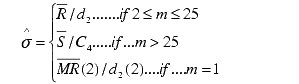
For variable subgroup sizes and m > 1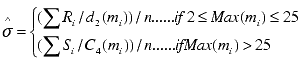 
where 
n is the number of subgroups.
|
|
|
|
Special Case 
for variable subgroup sizes (if max subgroup size lies between 2 to 100), where
|
|
Calculated average of the Sample averages in a user defined period. |
|
|
|
Average value of the sample set. (Synonymous with Process Mean.) |
Is the same as provided mean ( |
|
|
Calculated average of the Sample Ranges in a user defined period. Also called Mean Range. |
|
|
|
Used typically in a histogram to visually indicate observations beyond the 3 sigma limit. |
Mean value - 3 Sigma, Sigma = provided ( |
|
|
Used typically in a histogram to visually indicate observations beyond the 3 sigma limit. |
Mean value + 3 Sigma, Sigma = provided ( |
|
|
Process Sigma (S) |
The standard deviation of the process data. This ignores the existence of any subgroups and uses all individual data to calculate the standard deviation. |
|
|
Process Mean |
The average (mean) of the process data. This ignores the existence of any subgroups and uses all individual data to calculate the mean. |
|
|
Provided Mean |
Provided in the configuration dialog. Allows the user to
manually override |
N/A |
|
The maximum individual value in the sample set. |
MAX (x1, x2, ... xn) |
|
|
The minimum individual value in the sample set. |
MIN (x1, x2, ... xn) |
|
|
Moving Average smoothes your data by averaging consecutive observations in a series. This is useful when the data does not have a trend or seasonal component. |
The moving average of moving length w for subgroup t is defined as
|
|
|
Moving Length (w) |
A parameter used for the calculation of Moving Average and Moving Range to specify the number of consecutive observations. |
N/A |
|
Moving Range smoothes your data by averaging consecutive ranges in a series. This is useful when the data does not have a trend or seasonal component. |
The moving range of moving length w for subgroup t is defined as
|
|
|
Frequency |
Number of observations for each data category. |
N/A |
|
Cumulative Frequency |
Sum of frequencies of the current category and all those with higher frequencies (Pareto chart). |
|
|
Cumulative Percentage |
Cumulative frequency divided by the total of frequencies (Pareto chart). |
|
|
Data Mean |
Mean of c, u, p or np values (attribute charts). |
N/A |
|
Data Sigma |
Sample deviation of c, u, p or np values (attribute charts). |
N/A |
|
Sample Data |
Section of exported data, including raw data, control limits, data exclusion status and alarm test results. |
N/A |
|
Total number of samples. |
N/A |
|
|
SubGroup Means |
The mean value of each subgroup. |
See XbarBar Definition. |
|
Subgroup Ranges |
The Range value of each subgroup. |
See Rbar Definition. |
|
Subgroup Sigmas |
The Sigma (standard deviation) value of each subgroup. |
See Estimated Sigma Definition. |
|
The desired value of a product or process measurement. |
N/A |
|
|
Upper Specification Limit, or Upper Spec Limit, is a value above which performance of a product or process is unacceptable. |
N/A |
|
|
Lower Specification Limit, or Lower Spec Limit, is a value below which performance of a product or process is unacceptable. |
N/A |
|
|
A capability indicator for a stable process. Cp measures the process capability ratio.
The Cp index is used to summarize a system's ability to meet two-sided specification limits (upper and lower). Like Cpk, it uses estimated sigma and, therefore, shows the system's potential to meet the specifications. However, it ignores the process average and focuses on the spread. If the system is not centered within the specifications, Cp alone may be misleading.
The higher the Cp value the smaller the spread of the system's output relative to the specification limits. A process with a high Cp value may not meet customer needs if it is not centered within the specifications.
A capability indicator for a stable process. Cp measures the process capability ratio.
|
|
|
|
|
The Cp index is used to summarize a system's ability to meet two-sided specification limits (upper and lower). Like Cpk, it uses estimated sigma and, therefore, shows the system's potential to meet the specifications. However, it ignores the process average and focuses on the spread. If the system is not centered within the specifications, Cp alone may be misleading.
The higher the Cp value the smaller the spread of the system's output relative to the specification limits. A process with a high Cp value may not meet customer needs if it is not centered within the specifications.
If the system is centered on its target value Cp should be used in conjunction with Cpk to account for both spread and centering. Cp and Cpk will be equal when the process is centered on its target value. If they are not equal, the smaller the difference between these indices, the more centered the process is. |
|
|
Also called Process Capability Index. The Cpk index compares the normal process variation to the specification range. If the process variation band exactly matches the specification range, the Cpk index is 1.0. The higher the Cpk, the more capable the process is of routinely meeting specification. A general rule of thumb is that a Cpk of at least 1.3 is desirable. The Cpk is the lesser of the two Cp Indices for individual specifications.
Cpk is a capability index that tells how well a system can meet specification limits. Cpk calculations use estimated sigma and, therefore, show the system's "potential" to meet specifications. Since it takes the location of the process average into account, the process does not need to be centered on the target value for this index to be useful.
If Cpk is 1.0 the system is capable of producing 99.73% of its output within specifications. The larger the Cpk, the less variation you will find between the process output and specifications.
|
|
|
|
|
Cpk should be used in conjunction with the Cp index. Cpk and Cp will be equal when the process is centered on its target value. If they are not equal, the smaller the difference between these indices, the more centered the process is. |
|
|
A capability index that compares process variation to the lower specification. |
|
|
|
A capability index that shows process stability within specifications in addition to the target.
The Cpm index indicates how well the system can produce within specifications. Its calculation is similar to Cp. The larger the Cpm, the more likely the process will produce output that meets specifications and the target value. |
T is the Target value. If Target is not available, T = (USL+LSL)/2 If |
|
|
A capability index that compares process variation to the upper specification. |
|
|
|
A capability ratio for a stable process. The reciprocal of Cp.
The Cr capability ratio is used to summarize the estimated spread of the system compared to the spread of the specification limits (upper and lower). The lower the Cr value, the smaller the output spread. Cr does not consider process centering.
When the Cr value is multiplied by 100, the result shows the percent of the specifications that are being used by the variation in the process. Cr is calculated using an estimated sigma and is the reciprocal of Cp. In other words, Cr = 1/Cp. |
|
|
|
The Pp index is used to summarize a system's performance in meeting two-sided specification limits (upper and lower). Like Ppk, it uses process sigma (standard deviation of the individual values), and shows how the system is actually running when compared to the specifications. However, it ignores the process average and focuses on the spread. If the system is not centered within the specifications, Pp alone may be misleading.
The higher the Pp value the smaller the spread of the system's output relative to the specification limits. A process with a narrow spread (a high Pp) may not meet customer needs if it is not centered within the specifications.
Pp should be used in conjunction with Ppk to account for both spread and centering. Pp and Ppk will be equal when the process is centered on its target value. If they are not equal, the smaller the difference between these indices, the more centered the process is. |
|
|
|
Ppk is an index of process performance that tells how well a system is meeting specifications. Ppk calculations use process sigma (standard deviation of the individual values), and shows how the system is actually running when compared to the specifications. This index also takes into account how well the process is centered within the specification limits.
If Ppk is 1.0 the system is producing 99.73% of its output within specifications. The larger the Ppk, the less the variation between process output and specifications.
Ppk should be used in conjunction with the Pp index. If the system is centered on its target value, Ppk and Pp will be equal. If they are not equal, the smaller the difference between these indices, the more centered the process is. |
|
|
|
A performance index that compares process variation to the lower specification. |
|
|
|
A performance index that compares process variation to the upper specification. |
|
|
|
A performance ratio for a process. The reciprocal of Pp.
The Pr performance ratio is used to summarize the actual spread of the system compared to the spread of the specification limits (upper and lower). The lower the Pr value, the smaller the output spread. Pr does not consider process centering.
When the Pr value is multiplied by 100, the result shows the percent of the specifications that are being used by the variation in the process. Pr is calculated using the actual sigma (sigma of the individuals) and is the reciprocal of Pp. In other words, Pr = 1/Pp. |
|
|
|
The number of samples above the upper specification limit. Number of observations higher than the upper specification limit. |
N/A |
|
|
The number of samples below the lower specification limit. Number of observations lower than the lower specification limit. |
N/A |
|
|
The number of samples outside of the upper and lower specification limits. |
OOSHigh + OOSLow |
|
|
The percentage of Data in the current population above the Upper Specification Limit. Percentage of the number of observations higher than the upper specification limit. |
N/A |
|
|
The percentage of Data in the current population below the Lower Specification Limit. Percentage of the number of observations below the lower specification limit. |
N/A |
|
|
The percentage of Data in the current population outside of the Upper and Lower Specification Limits. Total percentage of the number of observations below the lower specification limit and higher than the upper specification limit. |
% OOSHigh + % OOSLow |
|
|
The expected percentage of data rising above the upper specification limit based on the Normal Distribution fitted on sample data. |
100*( |
|
|
The expected percentage of data falling below the Lower specification limit based on the Normal Distribution fitted on sample data. |
100*( |
|
|
The expected percentage of data falling outside the Upper and Lower Specification Limits based on the Normal Distribution fitted on sample data. |
Estimated % OOSHigh + Estimated % OOSLow |
|
|
A measure of the concentration of a distribution around its mean. Kurtosis is used to determine whether data is peaked or flat relative to a normal distribution. A positive value means a distinct peak near the mean; negative means a flat distribution. |
|
|
|
A measure to determine the symmetry of the histogram; 0 means symmetric, negative means skewed left, and positive means skewed to right. |
|
|
|
Indicates whether the population is accepted as being part of a normal distribution. A higher P value implies that there is a greater chance the data is normal. |
Anderson-Darling Normality
Test The test performed - Null Hypothesis H0: data follows Normal Distribution vs. Alternative Hypothesis H1: data does not follow Normal distribution.
Calculate Test Statistic n = number of values in Y, and
Y is the ordered data from y. X ~ Normal
|
|
|
|
|
Calculate P-Value The cumulative distribution function of the Anderson-Darling test statistic is calculated using a saddle point approximation algorithm as described below. (Algorithm Reference: A Saddlepoint Approximation to the Distribution Function of the Anderson-Darling Test Statistic, by David E. A. Giles, Department of Economics, University of Victoria, B.C., Canada, April, 2000). Find cumulant generating function for A2
where lj = 1/(j(j+1)) First two derivatives of the cumulant generating function are:
Now we solve the saddle point equation
The saddlepoint approximation of c.d.f of A2 (i.e., P-Value) is
where,
|
|
Also known as "Long Term Capability", represents the sustained reproducibility of a process. In context of the Six Sigma Program, it is the value used to estimate the long-term process "PPM". It reflects the influence of special cause variation, dynamic nonrandom process centering error, and any static offset present in the process mean. It is a measure of how well the process is controlled (over how many cycles) when compared to Z(Bench) ST. A process having a Z(bench)LT of 4.5 produces 3.4 defects per million opportunities. |
|
|
|
Also called "Short-Term Capability" or "Instantaneous Capability", this value describes how precise the process is at any given time. In the context of the Six Sigma Program, it is the value used when referring to the "SIGMA" of a process. It represents the true potential of the process technology to meet the given performance specification(s) (i.e., what the process can do if everything is controlled to such an extent that only background noise is present, common cause variation). |
|
|
|
The Z score for an item relative to its lower specification limit. It indicates how far the process varies from the lower specification limit with respect to the process standard deviation. |
|
|
|
The Z score for an item relative to its lower specification limit. It indicates how far the target varies from the lower specification limit with respect to the estimated standard deviation. |
|
|
|
The Z score for an item relative to its upper specification limit. It indicates how far the process varies from the upper specification limit with respect to the process standard deviation. |
|
|
|
The Z score for an item relative to its upper specification limit. It indicates how far the target varies from the upper specification limit with respect to the estimated standard deviation. |
|
|
|
A basic calculation of the long term process performance analogous to Z(Bench) LT. Equivalent to "Z LT" calculated in ShopFloor SPC. |
3 * Ppk |
|
|
Z(Min) ST |
A basic calculation of the short term estimated capability analogous to Z(Bench) ST. Equivalent to "Z ST" calculated in ShopFloor SPC. |
3 * Cpk |
|
|
|
|
|
|
|
|
|
SYMBOLS |
|
|
|
|
Inverse Normal Distribution function (i.e., given probability it finds the standard Normal Z value). |
N/A |
|
|
ith data of the jth subgroup. |
N/A |
|
n |
Number of subgroups. |
N/A |
|
m |
Subgroup size in case of uniform subgroup size. |
N/A |
|
mi |
ith subgroup size in case of variable subgroup sizes. |
N/A |
|
k |
Multiplication factor (default is 3.0). |
N/A |
|
|
Mean Moving Range of length w (Average of Ranges taken with moving length of w). |
N/A |
|
|
Standard Normal cdf (i.e., Prob(X |
|
|
|
Standard Normal density function where X follows Normal(0, 1). |
|
= Mean Range (Average of subgroup Ranges)
= Mean Moving Range
of length 2 (Average of Ranges taken with moving length of 2)
is the ith subgroup Range
is the
ith subgroup Sigma
is the
ith subgroup size and n is the number of
subgroups
as 
for uniform subgroup size (values 2-100) and
for uniform subgroup sizes.
for variable subgroup sizes.
, where 
is the ith subgroup mean,
xij is jth observation of
ithsubgroup for uniform subgroup sizes (i.e., all
mi's are the same).
for variable subgroup sizes.
) if given, otherwise 
(Mean of subgroup Means)
is used.
, where 
is the ith subgroup Range, and n is the
number of subgroups. Range is ABS (max - min).
) if given, otherwise
Estimated Sigma (
) is used.
) if given, otherwise
Estimated Sigma (
) is used.
, where xi is individual
observations, and n is the total number of observations,
and 
is Process Mean.
.
, where 
=kth subgroup mean.
, where 
=kth subgroup range.
where
where
n = total number
of categories.
and 
is not given use 
and 
respectively.
)
)
is the Normal Cumulative Distribution function (cdf),
(i.e., P(X
x)).
(t) = y
for t by Newton-Raphson method, and use the solution (
) to evaluate the following:
, where sign(x)=1 if x>0, -1 if x<0 and 0 id
x=0
and 
are standard Normal cdf and density functions
respectively.
, t =
Target value if given, otherwise t = (usl+lsl)/2
, t =
Target value if given, otherwise t = (usl+lsl)/2
x), where X follows
Normal(0, 1)).
where 